Esta página contiene un conjunto de apuntes sobre la criptografía demostrablemente segura (provably-secure cryptography), pensados para estudiantes de pregrado en computación, ingeniería, física o matemática.
Estos apuntes cubren primitivas estándar fundamentales para proteger las comunicaciones en línea. Cada primitiva es acompañada por una construcción de ejemplo, elegida por ser simple de demostrar segura.
Estos apuntes intentan cubrir un hueco en la literatura: la falta de apuntes sobre criptografía moderna demostrablemente segura en español. Asimismo, intentan enfrentar el argumento de la manera conceptualmente más simple posible, otorgando al mismo tiempo garantías formales y rigurosas.
Los actuales apuntes son un boceto inicial, con limitaciones conocidas y probablemente varios defectos aún por identificar.
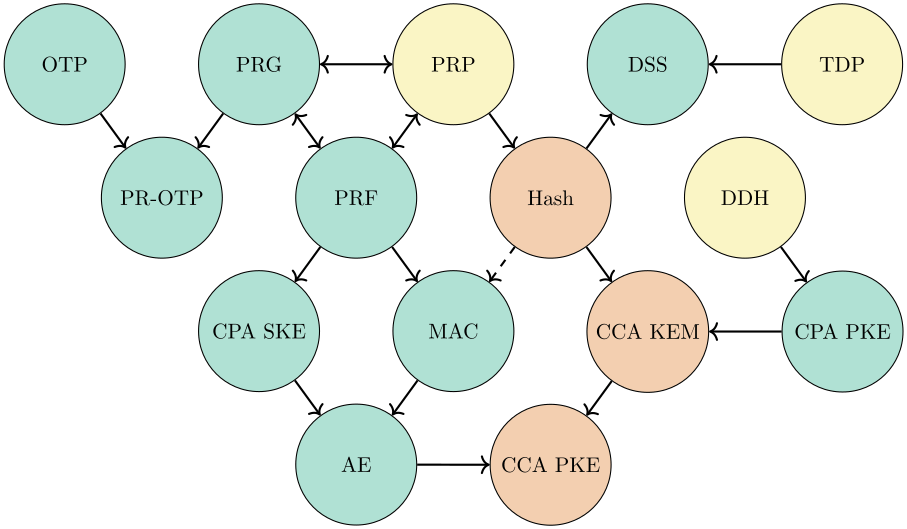
El curso cubre solamente el diseño (o construcción) de primitivas criptográficas, basándose sobre tres postulados computacionales, o suposiciones de dificultad, que vienen introducidos en los apuntes, pero no cuestionados en detalle:
- la existencia de permutaciones pseudoaleatorias,
- la existencia de grupos cíclicos con problema decisional de Diffie-Hellman difícil,
- la existencia de permutaciones de puerta trasera.
Descargas
Apuntes
- Archivo de apuntes completo (menos diapositivas): apuntes.pdf
- Clase 0 (diapositivas): introducción
- Clase 1: Probabilidad y aleatoriedad
- Clase 2: cifrado simétrico, one-time pad (OTP)
- Clase 3: generadores pseudoaleatorios (PRG)
- Clase 4: seguridad computacional y one-time-pad pseudoaleatorio
- Clase 5: funciones pseudoaleatorias (PRF)
- Clase 6: cifrados de bloque (PRP)
- Clase 7: las PRP son PRFs
- Clase 8: confidencialidad multi-mensaje, "counter mode" (CTR)
- Clase 9: el counter mode es seguro
- Clase 10: funciones de hash y contraseñas
- Clase 11: integridad y códigos de autenticación de mensajes (MAC)
- Clase 12: cifrado autenticado (AE)
- Clase 13: grupos finitos, logaritmo discreto (DLOG)
- Clase 14 (diapositivas): intercambio de claves Diffie-Hellman (DH KEX)
- Clase 15: cifrado asimétrico (PKE)
- Clase 16: seguridad multi-mensaje asimétrica
- Clase 17: cifrado asimétrico contra adversarios activos
- Clase 18: cifrado híbrido (KEM-DEM), transformada de Fujisaki-Okamoto (FO)
- Clase 19: firmas digitales (DSS)
- Clase 20: firmas Full-Domain Hash (FDH)
- Clase 21 (diapositivas): infraestructura de claves publica (PKI)
Más información
Motivación
Las comunicaciones en línea son omnipresentes en la sociedad digital contemporánea. La criptografía, la familia de técnicas utilizadas para proteger tales comunicaciones, es una materia a menudo poco entendida, y raramente enseñada en detalle en cursos de pregrado. Al mismo tiempo, los mecanismos de seguridad criptográficos son fácilmente utilizados de manera incorrecta, con consecuencias severas.
Objetivos
- Proporcionar a los estudiantes una visión de la funcionalidad criptográfica necesaria para lograr comunicaciones cifradas básicas de uno a uno a través de Internet.
- Mostrar el modelado de amenazas criptográficas y las formas sutiles en que el diseño criptográfico puede fallar.
- Demostrar cómo tratar formalmente las primitivas criptográficas para demostrar garantías de seguridad a través de teoremas.
Resultados
- El estudiante aprenderá los componentes estrictamente necesarios para construir un canal seguro básico en una red pública.
- Para cada componente, el estudiante comprenderá formalmente al menos una construcción y podrá argumentar su seguridad.
- A través de la comprensión de los componentes básicos utilizados en la criptografía moderna, el estudiante estará preparado para comprender protocolos más complejos usados en la práctica, como TLS y SSH, y la necesidad de tener precaución al construir aplicaciones criptográficas.
Requisitos
En los apuntes cubrimos los fundamentos matemáticos necesarios. Tratamos de incluir solamente los requisitos matemáticos indispensables, en un intento de que los apuntes sean lo más accesibles posible, y que al mismo tiempo sean rigurosos.
La primera mitad del curso requiere una comprensión básica de la probabilidad, y en particular de la noción de probabilidad condicional.
La segunda mitad del curso cubre un poco de teoría básica de grupos. Esta se encuentra incluida en el material.
Organización
El material corriente se encuentra dividido en 19 "clases", cada una de aproximadamente 1 hora de material, y de 3 conjuntos de diapositivas, correspondiente en total a aproximadamente 2 horas de material.
Desafortunadamente, en este momento los apuntes no incluyen ejercicios.
Temario
El temario está dividido en 12 componentes, que llevarán les estudiantes de no tener bases en criptografía, a conocer los componentes basilares requeridos para comunicaciones confidenciales por internet.
Criptografía simétrica (o “de clave secreta”)
- Repaso sobre probabilidad, introducción de: la noción de secreto perfecto, el cifrado de un solo uso (One-Time Pad), teorema de Shannon.
- Juegos de seguridad, definición de generador de números pseudoaleatorios (PRG), noción formal de seguridad de PRG, definición de cifrado similar a OTP usando un PRG.
- Definición de cifrado de bloque o permutación pseudoaleatoria, de función pseudoaleatoria, de noción de seguridad semántica (IND-CPA), demostración de seguridad del modo de uso CTR.
- Códigos de autenticación de mensajes (MAC), noción seguridad MAC, PRFs como MAC, funciones de hash.
- Maleabilidad de cifrados IND-CPA, noción de integridad de cifrado (INT-CTXT) y de cifrado autenticado (AE). Cifrado Encrypt-then-MAC (EtM), demostración de que EtM proporciona un cifrado autenticado.
Criptografía asimétrica (o “de clave pública”)
- Distribución de claves secretas y la criptografía de clave pública; hipótesis de complejidad computacional DLOG, CDH, DDH.
- Definición de cifrado de clave pública (PKE), definición de seguridad semántica PKE, hipótesis DDH, PKE de ElGamal, demostración de que Elgamal es seguro IND-CPA basado en DDH.
- Definición de mecanismo de encapsulamiento de claves (KEM), ataques de cifrado elegido en PKE y KEMs, nociones de seguridad PKE y KEM IND-CCA.
- Transformación KEM CPA -> KEM CCA de Fujisaki-Okamoto. Construcción de PKE IND-CCA a partir de KEM y de AE.
- Ataques máquina-en-el-medio (MITM) y la necesidad de autenticación de claves públicas, firmas digitales, infraestructura de claves públicas (PKI).
- Noción de infalsificabilidad (“strong unforgeability”, SUF-CMA), funciones de puerta trasera.
- Firmas de dominio completo de hash (“Full-Domain Hash”, FDH), demostración de seguridad de FDH. Reflexiones finales: ¿hemos terminado? Realmente, no. ¡Muchos problemas abiertos!
Bibliografía
El material de los apuntes es estándar, y se puede encontrar tratado en varios libros de texto. Los recomendados (y usados para preparar los apuntes) son
- Dan Boneh and Victor Shoup, "A Graduate Course in Applied Cryptography", autoeditado y de libre acceso en https://toc.cryptobook.us
- Mike Rosulek, "The Joy of Cryptography", autoeditado y de libre acceso en https://joyofcryptography.com
- Jonathan Katz and Yehuda Lindell, “Introduction to Modern Cryptography”, tercera edición, CBC Press
- Nigel Smart, “Cryptography, an Introduction”, tercera edición, autoeditado y de libre acceso en https://nigelsmart.github.io/Crypto_Book/
Cursos enseñados usando estos apuntes:
- Optativa de Criptografía Moderna, Departamento de Computación de la Universidad de Buenos Aires, mayo de 2025.
- Optativa de Criptografía Moderna, Departamento de Computación de la Universidad de Buenos Aires, abril de 2024.